机器学习基础教程

本文基于DorsaRoh/Machine-Learning仓库，提供了机器学习基础知识的系统性介绍，包括神经网络和Transformer模型的原理与实现。这份教程特别适合希望从零开始理解机器学习核心概念的学习者。

神经网络基础

什么是神经网络？

神经网络是由多个神经元组成的计算模型，这些神经元按层组织：

1. 输入层：接收初始数据
2. 隐藏层：处理数据的中间层
3. 输出层：产生最终结果

每个神经元都持有一个数值，称为"激活值"。

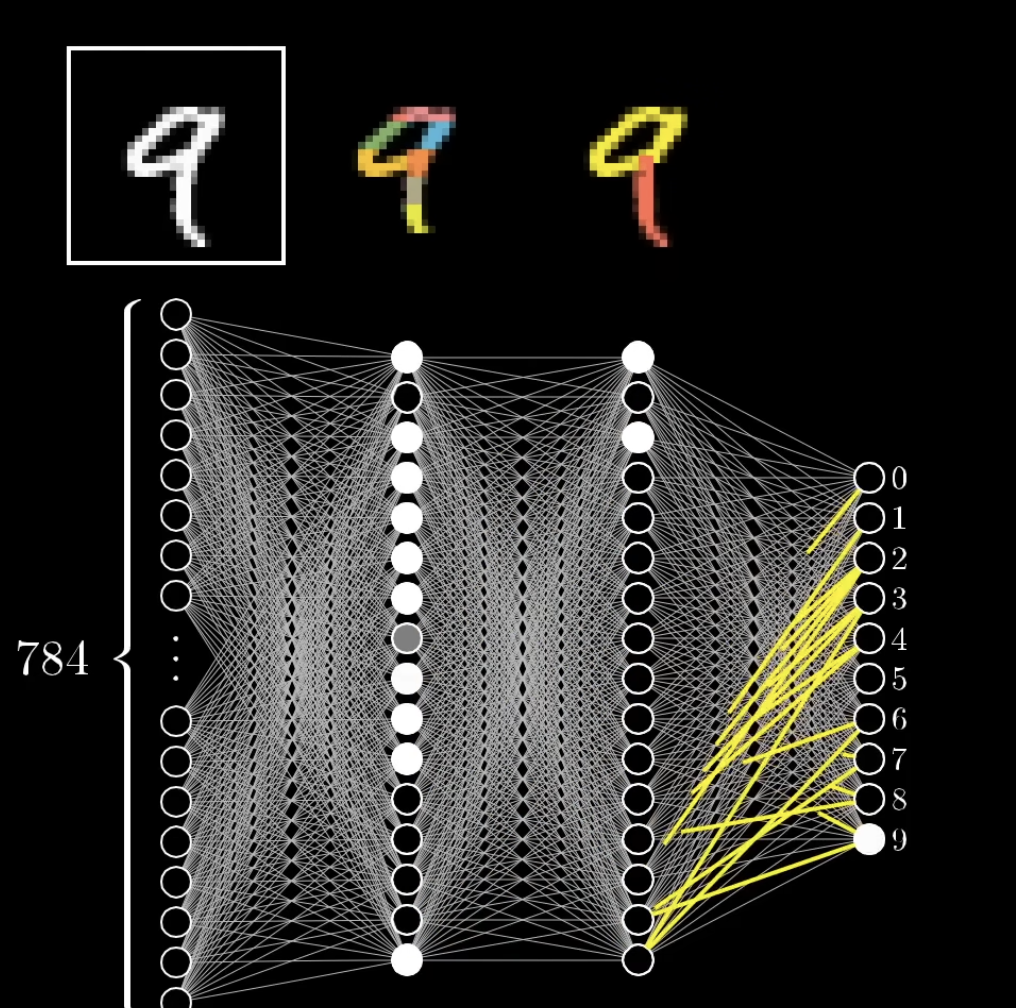
神经网络如何工作？

神经元之间的连接

• 一层中的每个神经元都与下一层的所有神经元相连
• 每个连接都有一个"权重"，表示连接的强度
• 在训练过程中，这些权重会被调整以识别数据中的模式

神经元激活值的计算

神经元的激活值基于以下因素计算：

1. 前一层所有神经元的激活值
2. 与这些神经元的连接权重

计算过程：

1. 将每个输入激活值乘以相应的权重
2. 将所有这些乘积相加
3. 加上一个特殊值，称为"偏置"

这可以用公式表示：

加权和 = w1*a1 + w2*a2 + ... + wn*an + 偏置

其中：

• wi 是与前一层神经元 i 的连接权重
• ai 是前一层神经元 i 的激活值
• 偏置是一个额外的可调整值

偏置的作用

偏置有重要的功能：

• 它移动激活函数
• 这使神经元能够调整其对输入的敏感度
• 正偏置使神经元更容易激活
• 负偏置使神经元不太容易激活

激活函数

计算加权和后，我们应用"激活函数"。常见的选择包括：

1. Sigmoid函数：将输出映射到0到1之间
2. ReLU（修正线性单元）：如果输入为正，则输出输入值；否则输出0

ReLU函数的Python实现：

def relu(self, x):
    return np.maximum(0, x)

ReLU很受欢迎，因为它有助于网络更有效地学习。

训练神经网络

前向传播

这是将输入通过网络传递以获得输出的过程：

1. 从输入层开始
2. 对于每个后续层： a. 计算每个神经元的加权和 b. 应用激活函数
3. 重复直到达到输出层

衡量性能：损失函数

为了训练网络，我们需要衡量它的表现。我们使用损失函数：

1. 比较网络的输出与期望输出
2. 计算差异
3. 对这个差异进行平方（使所有值为正）
4. 对所有输出神经元的平方差求和

结果称为"损失"。损失越小，网络表现越好。

def mse_loss(self, y, activations):    
    return np.mean((activations-y)**2)

梯度下降和反向传播

为了提高网络的性能，我们需要调整其权重和偏置。我们使用两个关键概念：

1. 梯度下降：一种最小化损失的方法
2. 反向传播：一种计算如何调整每个权重和偏置的算法

工作原理：

1. 计算损失函数的梯度
   • 这告诉我们改变每个权重和偏置如何影响损失
2. 在减少损失的方向上更新权重和偏置
3. 重复这个过程多次

梯度下降

• 优化算法，用于最小化成本函数
• 使用梯度来更新/调整权重和偏置，使成本最小化
• 我们寻找成本函数的负梯度，它告诉我们如何改变权重和偏置以最有效地降低成本

反向传播是用来计算这些梯度的算法

反向传播

反向传播是确定单个训练样例如何调整权重和偏置的算法，不仅是它们应该上升还是下降，还包括这些变化的相对比例，以使成本最快地下降。

• 梯度的大小表示成本函数对每个权重和偏置的敏感度
  • 例如，你有梯度[3.2, 0.1]。调整梯度为3.2的权重会导致成本变化是调整梯度为0.1的权重时成本变化的32倍

激活值受三种方式影响：
w1a1 + w2a2 + ... + wn*an + 偏置

• 改变偏置
• 增加权重，与其激活值成比例（激活值越大，变化越大）
• 改变前一层的所有激活值，与其权重成比例（权重越大，变化越大）
  • 但我们不能直接影响激活值本身，只能影响权重和偏置

"向后传播"：反向传播从最后一层向第一层应用。

∂C/∂w = ∂C/∂a × ∂a/∂z × ∂z/∂w

其中C是成本，w是权重，a是激活值（神经元的输出），z是加权和（神经元的输入，在激活前）。

这告诉我们，如果我们稍微调整特定权重，成本（误差）会如何变化。

• 它指示了改变权重的方向。如果导数为正，减少权重将减少误差，反之亦然。
• 大小告诉我们误差对这个权重变化的敏感度。较大的大小 = 权重对误差有更大的影响

完整的Python实现

以下是用Python从头开始实现神经网络（前馈多层感知器）的基本实现：

Neuron类：

• 实现带有ReLU激活的前向传递
• 实现反向传递，应用链式法则
• 基于计算的梯度更新权重和偏置

Layer类：

• 管理神经元集合
• 为整个层实现前向和反向传递

NeuralNetwork类：

• 管理多个层
• 实现通过所有层的前向传递
• 实现训练循环，包括：
  • 前向传递
  • 损失计算
  • 反向传递（反向传播）
  • 所有权重和偏置的更新

import numpy as np

class Neuron:
    def __init__(self, num_inputs):
        self.weights = np.random.randn(num_inputs, 1) * 0.01
        self.bias = np.zeros((1, 1))
        self.last_input = None
        self.last_output = None

    def relu(self, z):
        return np.maximum(0, z)
    
    def relu_derivative(self, z):
        return np.where(z > 0, 1, 0)
    
    def forward(self, activations):
        self.last_input = activations
        z = np.dot(activations, self.weights) + self.bias
        self.last_output = self.relu(z)
        return self.last_output

    def backward(self, dC_da, learning_rate):
        da_dz = self.relu_derivative(self.last_output)
        dC_dz = dC_da * da_dz
        dC_dw = np.dot(self.last_input.T, dC_dz)
        dC_db = np.sum(dC_dz, axis=0, keepdims=True)

        self.weights -= learning_rate * dC_dw
        self.bias -= learning_rate * dC_db

        return np.dot(dC_dz, self.weights.T)

class Layer:
    def __init__(self, num_neurons, num_inputs_per_neuron):
        self.neurons = [Neuron(num_inputs_per_neuron) for _ in range(num_neurons)]

    def forward(self, activations):
        return np.hstack([neuron.forward(activations) for neuron in self.neurons])
    
    def backward(self, output_gradient, learning_rate):
        return np.sum([neuron.backward(output_gradient[:, [i]], learning_rate) for i, neuron in enumerate(self.neurons)], axis=0)

class NeuralNetwork:
    def __init__(self, layer_sizes):
        self.layers = []
        for i in range(len(layer_sizes) - 1):
            self.layers.append(Layer(layer_sizes[i+1], layer_sizes[i]))

    def forward(self, activations):
        for layer in self.layers:
            activations = layer.forward(activations)
        return activations
    
    def mse_loss(self, y, activations):    
        return np.mean((activations-y)**2)
    
    def derivative_mse_loss(self, y, activations):
        return 2*(activations-y) / y.shape[0]
    
    def train(self, X, y, epochs, learning_rate, batch_size=32):
        for epoch in range(epochs):
            total_loss = 0
            for i in range(0, len(X), batch_size):
                X_batch = X[i:i+batch_size]
                y_batch = y[i:i+batch_size]
                
                outputs = self.forward(X_batch)
                loss = self.mse_loss(y_batch, outputs)
                total_loss += loss * len(X_batch)

                output_gradient = self.derivative_mse_loss(y_batch, outputs)
                for layer in reversed(self.layers):
                    output_gradient = layer.backward(output_gradient, learning_rate)

            avg_loss = total_loss / len(X)
            print(f"Epoch {epoch+1}/{epochs}, Loss: {avg_loss}")

    def predict(self, X):
        return self.forward(X)

Transformer模型

概述

Transformer是一种强大的神经网络架构，特别适用于处理序列数据，如文本。以下是Transformer的关键组件和概念。

输入

一组实数，可以是：

• 简单列表、2D矩阵，甚至更高维度的张量
• 这组数字通过多个层逐步转换，每层都是一个实数数组，直到达到最终输出层
  • 例如，在像GPT这样的文本处理模型中，最终层生成一个数字列表，表示所有可能的下一个单词的概率分布

输出

所有潜在下一个标记的概率分布

标记（Tokens）

标记是信息的"小片段"（例如单词、单词组合、声音、图像）

• 每个标记都与一个向量（一些数字列表）相关联
  • 编码了该片段的含义
  • 例如，将这些向量视为坐标，含义相似的单词往往彼此靠近

嵌入（Embeddings）

在相同上下文中使用和出现的单词往往表达相似的含义（分布式语义学）

• 将输入分解成小块，然后转换为向量。这些小块称为标记
• 模型有预定义的词汇表（所有可能单词的列表）
• 嵌入矩阵（W_E）：每个单词一列
• 嵌入空间的维度可能非常高（例如12,288）
• 理论上，E(man) - E(woman) ≈ E(king) - E(queen)
• 两个向量的点积是它们对齐程度的度量。在这种情况下，这作为单词之间相似性的度量

下图是嵌入矩阵。每个单词对应一个特定的向量，没有参考其上下文。注意力块的责任是用上下文更新单词的向量。

位置编码（Positional Encoders）

位置编码提供关于序列中标记顺序的信息。

• 例如，特定单词在句子中的位置。
• 每个单词的嵌入都添加了一个固定的位置编码向量。

注意：单词嵌入和位置嵌入是分开的。单词嵌入捕获语义含义，而位置编码捕获标记的顺序

反嵌入（Unembedding）

在确定Transformer的期望输出（生成文本中可能出现的所有可能标记的概率分布）时，在特定数据集上训练良好的网络能够通过以下方式确定下一个最佳可能标记：

1. 使用矩阵（嵌入矩阵W_u）将上下文中的最后一个向量/嵌入映射到50k个值的列表（词汇表中的每个标记一个）
2. 将其归一化为概率分布的函数（softmax）

Softmax（归一化）

Transformer的期望输出是生成文本中可能出现的所有可能标记的概率分布

概率分布定义为0-1之间的数字序列，总和为1。Softmax可以给任何数字序列这些标准

import numpy as np

# 给定一个数字序列，每个项`i`

# softmax方程：e^i/(所有项的e^i之和)

# 概率分布：
# 1) 所有数字都是0-1之间的正数 (e^i)
# 2) 所有数字的总和 = 1 (所有项的e^i之和)

seq = [2, 4, 5]
print(np.exp(seq)/np.sum(np.exp(seq)))
# [0.03511903 0.25949646 0.70538451]

温度（Temperature）

在softmax中，添加到e的指数分母中的常数T可以使生成的文本更有创意

• 使softmax输出对0和1的极端值不那么极端
• 这使得生成的文本更加独特，每次生成都不同

注意力（Attention）

目标：使模型能够在为特定标记生成输出时关注输入序列的不同部分

注意力分数

表示一个单词应该给予序列中另一个单词多少关注（或注意力）的值

注意力块

根据上下文更新单词的嵌入向量。使信息从一个嵌入传输到另一个嵌入

在注意力之前，每个单词的嵌入向量是一致的，无论其上下文如何（嵌入矩阵）。因此，注意力的动机是根据其上下文（即周围的标记）更新单词的嵌入向量，以捕获这个单词的特定上下文实例

预测下一个标记的计算完全依赖于当前序列的最终向量

最初，这个向量对应于序列中最后一个单词的嵌入。当序列通过模型的注意力块时，最终向量被更新以包含整个序列的信息，而不仅仅是最后一个单词。这个更新后的向量成为整个序列的摘要，编码了预测下一个单词所需的所有重要信息

单头注意力（Single-Head Attention）

目标：一系列计算，产生一组新的精炼嵌入

例如，让名词吸收其相应形容词的含义

查询（Query）

查询：表示单头注意力正在询问当前单词的"问题"/"焦点" 例如，如果当前单词是句子"The cat sat on the mat"中的"cat"，"cat"的查询可能在问，"这个句子中的哪些其他单词（键）我应该关注以更好地理解cat？"

键（Key）

键：作为一个标准/参考点，与查询进行比较以确定每个单词的相关性

• 通过评估它们与查询的相似性/相关性，帮助模型理解哪些其他单词与当前单词相关/重要
• 例如，在句子"The cat sat on the mat"中，"sat"的键可能包含表示句子中动作/动词方面的信息
• "cat"的查询可能会与这个键进行比较，以确定"sat"与理解与"cat"相关的动作相关

注意力分数

注意力分数：告诉我们每个单词的相关性

• 即表示一个单词（查询）应该给予序列中另一个单词（键）多少关注/注意力的值
• 通过比较当前单词的查询向量与序列中所有其他单词（包括自身）的键向量来计算
• 分数表示对当前单词中每个单词的相关性/重要性

计算方法：查询和键向量之间的点积

• 点积越高：键对查询越"相关"
• 这意味着模型在形成查询单词的最终表示时，给予该单词的值向量更多的权重
• 例如，在句子"The cat sat on the mat"中，如果模型根据它们的查询-键关系发现"cat"与"sat"相关，那么"cat"对"sat"的最终理解会有更高的影响

输入：查询、键和值矩阵

输出：矩阵，其中每个向量是值向量的加权和，权重来自注意力分数（基于查询和键矩阵的点积）

步骤：

1. 创建权重矩阵（最初随机初始化。与嵌入维度相同）
2. 从embed.py获取查询、键值（即对（单词嵌入和位置编码）的向量应用线性变换，对每个标记使用权重矩阵）
3. 计算注意力分数（查询和键矩阵的点积）
4. 对注意力分数应用掩码
5. 对（掩码）注意力分数应用softmax（这称为归一化）
6. 使用注意力分数对值向量进行加权
7. 输出步骤6的结果

点积越高，查询对键（即句子中一个单词对另一个单词）的相关性越大

掩码（Masking）

掩码是为了防止在训练过程中后面的标记影响前面的标记。这是通过将旧标记的条目设置为负无穷来实现的。因此，当应用softmax时，它们变为0。

为什么要掩码？

• 在训练过程中，为了效率，每个可能的子序列都被训练/预测。
• 一个训练示例实际上充当了多个示例。
• 这意味着我们永远不希望允许后面的单词影响前面的单词（因为它们基本上"泄露"了下一步的答案/预测的答案）

值（Value）

值矩阵W_v乘以单词的嵌入，并将其添加到下一个单词的嵌入中

值本质上回答：如果一个单词与调整某物的含义相关，那么应该向该其他事物的嵌入中添加什么，以反映这一点？

值：如果根据注意力分数判断单词相关，则持有将传递给网络下一层的实际信息的向量

• 计算注意力分数后，这些分数用于加权值
• 然后这些值的加权和用作当前单词的输出
• 继续使用句子"The cat sat on the mat"，如果"sat"（键）被认为对"cat"（查询）重要，那么与"sat"相关的值将显著贡献于"cat"的最终表示
• 这有助于模型理解"cat"与"坐"的动作相关

多头注意力（Multi-Head Attention）

注意力块由许多并行运行的注意力头组成（多头注意力）

通过并行运行许多不同的头，我们给予模型学习上下文改变含义的多种不同方式的能力

换句话说，多个Self Attention类的实例并行运行，每个实例具有不同的权重矩阵

步骤：

1. 声明并行运行的多个Self Attention头/实例
2. 每个Self Attention的头/实例通过拥有自己的一组权重矩阵（W_q, W_k, W_v）关注输入的不同部分
3. 每个Self Attention头/实例的输出沿嵌入维度（每个Self Attention类的输入）连接
4. 连接的输出通过最终线性变换（权重矩阵）传递
   • 将所有头的信息组合成单一输出

为什么要连接并应用最终线性变换？

连接所有头的输出的原因是每个头都学习了关于输入的不同内容。通过连接，我们将这些见解组合成一个单一的、统一的表示

最终线性变换应用于这个连接的输出，以将其恢复到原始嵌入维度

a. 连接 在多头注意力中，每个头学习输入的不同方面，因为每个头在嵌入的不同部分（head_dim）上操作。通过连接所有头的输出，我们将这些不同的学习表示组合成一个单一向量，封装了所有这些不同的见解

b. 最终线性变换 最终线性变换，使用权重矩阵完成，将来自不同头的信息混合回原始embedding_dim的单一向量。这一步至关重要，因为它允许模型创建一个统一的表示，整合每个头学习的不同视角

结论

本教程提供了神经网络和Transformer模型的基础知识，从零开始解释了这些模型的工作原理。通过理解这些基础概念，你可以更好地理解现代机器学习和深度学习模型的工作方式。

如果你想深入学习，建议查看原始仓库中的代码实现和更多详细说明：DorsaRoh/Machine-Learning。

---

本文内容基于DorsaRoh/Machine-Learning仓库，感谢原作者的贡献。